关于Itween插值算法的一点研究

　　用Itween很久了，但是Itween有时候会有动画执行到一半卡住的问题，于是就想自己写一个动画系统来取代itween，但是又希望新的动画系统也能像itween上有许多丰富的插值算法，于是找了一些资料，把研究结果记录于下。

　　首先是itween算法的官方文档
　　itween 插值算法 官方文档 Lua(版)

　　关于itween插值算法的效果可以去这个网站查看
　　itween 插值算法 演示

　　这里分析几个itween的插值算法

//平方淡入
local function inQuad(t, b, c, d)
　　t = t / d
　　return c * pow(t, 2) + b
end

明确了几个参数的定义，那么这个插值算法的内容就很明确了
首先 t = t / d
那么 t 就变成了当前时间与总时间的比值，我们可以知道这个值在动画开始时是0，在动画结束时是1
我们把1和0分别带入公式得 (tips: pow是幂函数，这里意义是返回0的2次方)
t = 0 时
return c * pow(0,2) + b
= c * 0 + b
= b
我们可以看出当t = 0 时，这个算法返回的是 b(开始值)
同样我们把t = 1带入公式
t = 1 时
return c * pow(1,2) + b
= c * 1 + b
= c + b
返回的值是c + b (变化值 + 结束值)
在这里我们看到，经过化简，我们的插值算法在t = 0时刻返回开始值，在t = 1时刻返回结束值

如果t是在0到1之间呢
我们看一下t^2 （t的平方）在0到1区间的函数图像 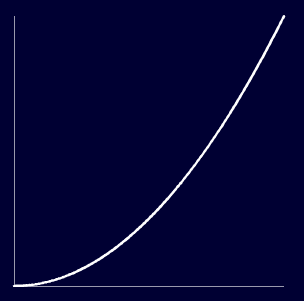我们看到t^2的值在0到0.5的范围内缓慢增长，0.5到1的范围内快速增长，所以这是一个先慢后快的插值算法。

我们再看一个

//回弹淡入
local function inBack(t, b, c, d, s)
  if not s then s = 1.70158 end
  t = t / d
  return c * t * t * ((s + 1) * t - s) + b
end

同样的，我们把t = 0 ,t = 1带入
化简公式得
t= 0 时
return c * 0 * 0 * ((s + 1) * 0 - s) + b
= b

t = 1 时
return c * 1 * 1 * ((s + 1) * 1 - s) + b
= c * ( s - s + 1) + b
= c + b

两个极值的返回值都符合我们预期，那么当t在0到1之间呢
我们先把函数中的b（开始值）去掉
c * pow(t , 2) * ( (s + 1) * t - s)

分析函数可以发现 当 t < s/(s + 1) 时 ( (s + 1) * t - s) < 0 ,函数为负值
t = s /(s + 1) 时，函数值为0
t = s /(s + 1) 时，函数值为正

s = 1.70158 时 s /(s + 1) 约等于0.62
由此我们可以得出结论
这个插值算法在前3分之2的时间都在向后退，然后在三分之二的时间回到原点，在最后3分之一的时间完成从起点到终点的插值
我们看一下这个插值算法 的图像
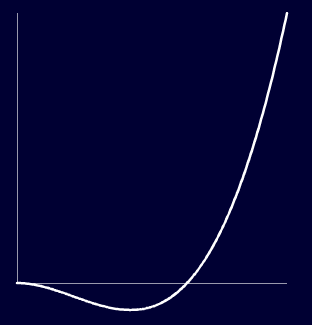基本上符合我们的预期，并且我们可以调整s的值来使我们回弹动画更快或者更慢。

另： 回弹的最低点位置在 ( 2 * s ) / 3 * ( s + 1 )位置，s = 1.7 时 t = 0.4。

最后我写了一个基于用lua写的动画系统，请看我的GitHub:

ok,我这篇文章就到这里，更多的插值效果请看官方文档 ^_^